We talk about the basics of WVR (Within Visual Range) engagements: turn performance, speed at merge, Specific Excess Power and much more.
Today we will try to bring you inside the mind of a fighter pilot engaging an adversary aircraft during a dogfight. And we will do that through a bit of the theory behind WVR aerial combat, explaining the so-called BFM (Basic Fighter Maneuvers), the tactical movements performed by a fighter during an aerial engagement to gain a positional advantage over the opponent. BFM are based on aerodynamic, physics, kinematics, energy and geometry concepts
Basic fighter maneuvers (BFM) are tactical movements performed by fighter aircraft during air combat maneuvering (also called ACM, or dogfighting), to gain a positional advantage over the opponent. BFM combines the fundamentals of aerodynamic flight and the geometry of pursuit, with the physics of managing the aircraft’s energy-to-weight ratio, called its specific energy.
Two great pillars have always been at the base of dogfights: the ONE CIRCLE FIGHT, also called “radius fight” or “nose to nose fight”; and the TWO CIRLCE FIGHT, also called “rate fight” or “nose to tail fight”. These represent two fundamental concepts of the doctrine that has reigned since the birth of aviation and that remain valid today. For this reason, although they have much evolved with the introduction of technological aids such as the HMD (Helmet Mounted Display) or aerodynamic aids such as TV (Thrust Vectoring), fighters pilots are still taught these basic concepts in their IFF (Introduction to Fighter Fundamentals) training.
Let’s start with the ONE CIRCLE FIGHT.
In this type of aerial engagement, both fighters fight on a “single circle” and tend to cross their tracks as shown in Fig. 1.
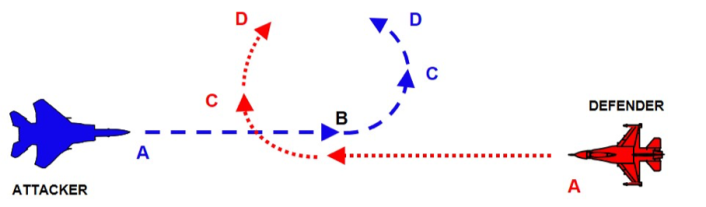
Everything starts with the “Blue” jet flying towards the “Red” in a neutral scenario (point A). At this point a fighter pilot already has in mind the “Game Plan”: the intention to enter into the fight and perform a “single circle” fight.
This type of fight is decided by the pilot who wants to use the excellent turning radius characteristics of his/her aircraft against a Red that is not as good in turn radius. Having said that, the pilot will tend to develop the fight upwards to reduce the airspeed to a minimum and, as a consequence, to reduce the turning radius [remember that the turning radius (r) is directly proportional to the square of the speed V2] as shown in Fig. 2.
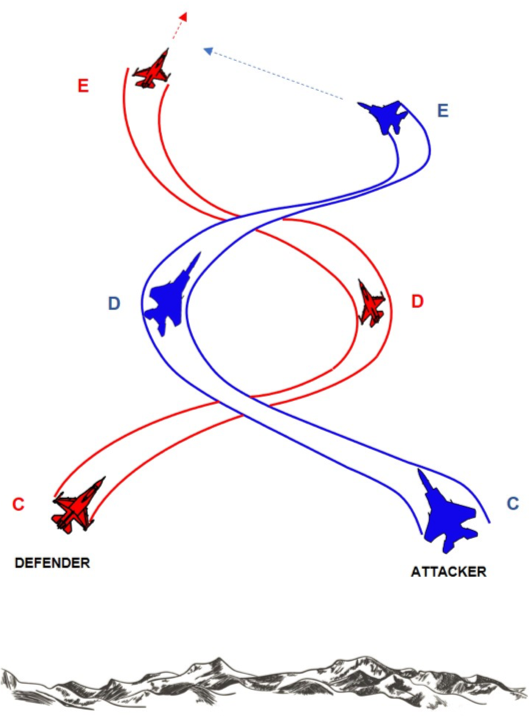
In addition, by setting a climbing maneuver at the time of the merge, the forward movement vector will also be reduced, thus increasing the chances of the pilot of finding hilmself/herself inside the turning radius of the defender.
Now let’s go back to beginning of the fight and imagine being inside the cockpit of the Blue jet. We have arrived at the merge head-on and the Red has now just flown to our six o’clock. We start a moderate abrupt pull-up maneuver to maintain the tally on the Red and we see him turning to our left. So we also turn to the left (point C in the figures). At this point, the challenge is to achieve the best performance (minimun turning radius) quicker than the enemy and maneuver within the Red plane’s turning radius.
As the fight develops (points C-D) the two aircraft will cross “nose to nose” in a maneuver called “flat scissors”: the aircraft that is capable of reaching first the smallest turning radius as well as the smallest forward movement will be able to obtain a shooting solution by pointing its nose at the other fighter (that in our case occurs at point E).
Now forget the points A-B-C-D-E because we are going to use the same to analyze the fight using, as an example, the F-16 turning performance tables below, where A, B, C would have a different meaning.
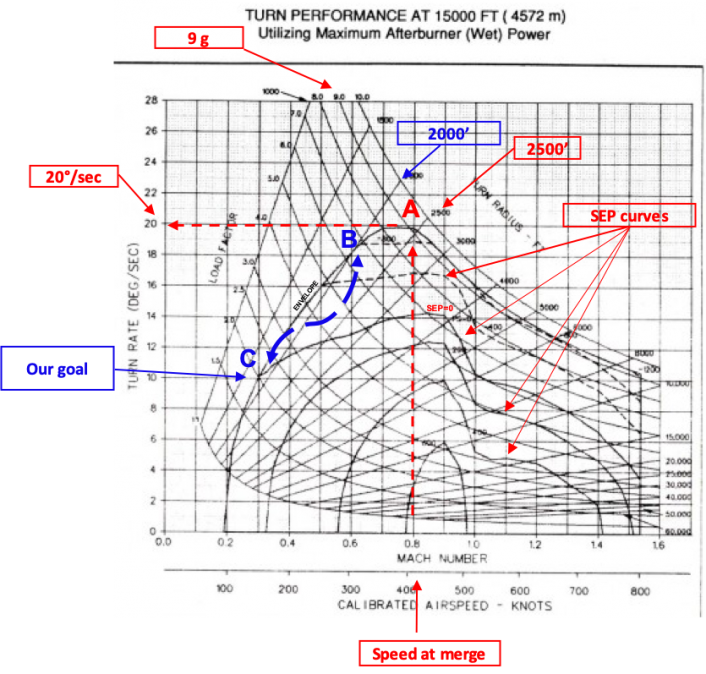
If you follow the red dotted line on the chart you can see that to get the best turn performance, the aircraft needs to reach the merge at around 430÷450 Kts/0.8 Mach. This would translate into a turning radius of 2,500 ft, a rate of 20 deg./sec and the ability to maneuver at 9G load factor (point A). Immediately after the merge, as we said, the pilot would start to turn with the purpose to achieve the minimum turn radius: in order to that he/she would pull Gs in the vertical, performing a maneuver to bring the aircraft at 300 kts/0.6 Mach: the pilot “aims” to reach point B of the chart, where the line that shows a minimum turning radius of 2,000 Ft is tangent to the line that represents the lower limit of the flight envelope of the aircraft. In point B, the aircraft can maintain a 18 degree turn rate and achieve the minimum turn rate. However these conditions are only sustainable for a moment so if the pilot wants to stay close to the minimum turn rate he/she would have to follow the blue line (the dotted one or a similar one – what is important is that from B to C the values on the x and y axis are not to the left of the continuous line that represents the boundary of the flight envelope) after merge and reduce speed and turn rate: at a 150 kts /0.3M the turn rate is 10 deg/sec and the minimim turn radius is below 2,000 feet. The aircraft is in point C where the flight envelope line intersects the curve for “SEP=0” (Specific Excess Power): it doesn’t need extra power to maintain speed and altitude while turning at the minimum turn radius. If the pilot is able to get to these points, he/she would be exploiting the aircraft at its best, as needed in a dogfight.
After this brief warm up analysis, the reader should have understood some basic concepts of the dogfighting doctrine. So, we can move on and see what happens in the TWO CIRCLE FIGHT, or the “rate fight”, looking at fig 4.
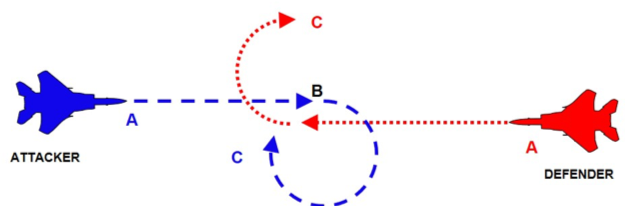
We are always in the cockpit of the blue aircraft about to get into the merge, but this time we know that we can fight and win on the red aircraft if we go for a two-circle fight because our plane has a better turn rate than the enemy.
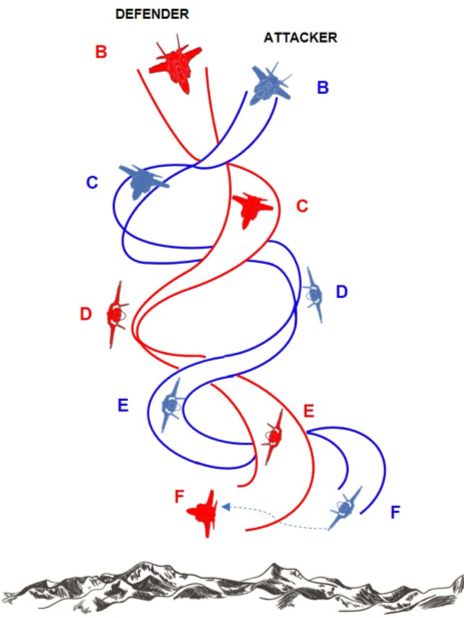
Returning now to our maneuver diagram, this time our target is to obtain the highest rate of turn (the above limit of the flight envelope): 20 deg/sec. Therefore, our merge speed should be 430÷450 Kts/0.8M and the most important thing is to be able to maintain this speed throughout the fight. At this speed maintaining 20 deg/sec is not possible because the aircraft is on SEP < 0 curve: to maintain this rate of turn we should lose 800ft/sec and that’s why generally all two circle fights develop downwards (fig. 5).
If we want to translate all this concept into a fight manoeuvres at the merge, we will simply roll the aircraft in a direction below the horizon, pull max Gs (we used to say “Lift Vector below the horizon”) continuing in a spiral and take advantage of the altitude (exchanging altitude for speed) in order to keep the speed as close as possible to our goal.
An important thing is worth highlighting: imagine you are flying the maneuver as show in fig. 5. You are turning at 9g to keep the tally on the red which has just passed at your 6 o’clock. Your head is turned backwards to keep the enemy insight (because “who loses sight loses the fight”) while you spiral towards the ground at the max performance, without looking at the HUD or flight instruments. It’s pretty obvious that fatigue can play a significant role here and this type of fight is often won by the fighter pilot who has the better G tolerance.
However, all these combat maneuvers often happen during the first few seconds of the fight (between 30 seconds and 1 minute into the fight); after hitting the 20 deg/sec (A), due to the progressive decrease of speed, we would be unable to maintain that turn rate. That’s why we should find a trade off that is called the “sustained speed”.
Let’s return to the turn performance diagram.
This time, after the merge and initial pull at 9g, our goal will be to use the altitude as much as we can and, when no altitude is available, keep the speed between 0.65M and 0.75M where we will touch the line with SEP=0, (B). From B, if we move along the SEP line between M0.65 and 0.75 (a range of speed called “sustained speed”) where we can fight without losing energy (speed or altitude or both ), turning at 14 deg/sec.
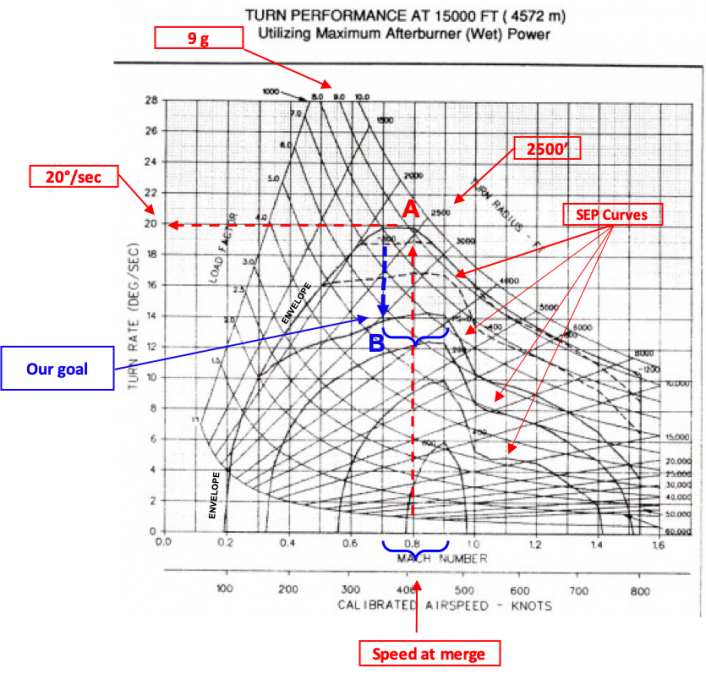
Normally you find yourself fighting at the “sustained speed” because you have reached the “combat floor” (and there’s no more altitude to trade): you can can “relax” so to speak and continue fighting at about 6 Gs.
Concluding, you should have now understood how a pilot studies the performance of both his/her jet and the opponent, how he/she sets some important flight parameters in his/her mind and we have introduced the doctrine of the rate fight and the radius fight. Air-to-air combat, however, is much more complex than described and it is not only made of the decisions set at the merge: the engagemenet is extremely dynamic and there’s a continuous change between one circle and two circle fight and vice versa. This means that the dogfight is not necessarily won by the pilot who flies the most performing aircraft but by the one who’s faster to put the aircraft at its maximum performance and change the type of fight when and if needed.
Fight’s on!









